I have been doing research in the field of theoretical nuclear physics, specifically on the low-energy structure and dynamics of the atomic nucleus and related quantum many-body problems. A prominent feature of the nucleus is that, even though it is a strongly correlated quantum many-body system (of protons and neutrons), it exhibits collective motions such as the vibrations of a spherical nuclear surface and the rotations of a deformed ellipsoid. The collective motions are observed as the characteristic energy spectra and electromagnetic transitions obeying the remarkable regularities and symmetries, which are also associated with certain geometrical shapes resembling a lemon (prolate), an orange (oblate), a pear (octupole), and so on. Since in the nuclei all the fundamental interactions in nature (except for the gravitational) play a significant role, studying the properties of the nuclei serves as a testing ground for possible new physics beyond the Standard Model of elementary particles, and helps deepening our understanding of the origin of matter, i.e., syntheses of heavy chemical elements.
How the atomic nucleus organizes itself into a variety of geometrical shapes? What are the microscopic mechanism behind? These are a central problem in nuclear physics, and are also common to finite quantal systems in general. My research has been mainly devoted to answer these questions, and to the development of a theoretical framework that allows for a microscopic, as well as consistent, description of the shapes and collective excitations in thousands of nuclear systems. Besides, using the knowledge of the nuclear theory I have pursued problems of fundamental importance that are common to the fields of nuclear, high-energy and astrophysics.
Interacting Boson Model
The Interacting Boson Model (IBM) has been remarkably successful in reproducing nuclear collective spectra. Its basic assumption is that the nuclear surface deformation is simulated in terms of bosons, which represent correlated pairs of valence nucleons. The model, on the other hand, should have its microscopic basis on nucleonic degrees of freedom, and attempts have been made to derive the boson model Hamiltonian from more fundamental nuclear structure models, e.g., the shell model. However, apart from the limited realistic cases of near spherical nuclei, a comprehensive method of deriving the IBM has not been known.

Based on the fact that the potential energy surface of the nuclear mean-filed model is simulated by that of the IBM, we have proposed a way of deriving the IBM Hamiltonian in the general situations of the quadrupole collective mode, covering near spherical vibrational, strongly deformed rotational, and γ-unstable states. Under the assumption that a given mean-field model (e.g., Skyrme, Gogny, relativistic, etc.) provides for all nuclei the correct intrinsic properties, the IBM can be derived, in principle, for arbitrary nuclei including those for which experimental data do not exist. Unlike conventional IBM, we are now in a position to make a quantitative prediction on the spectroscopy of exotic nuclei in heavy-mass regions.
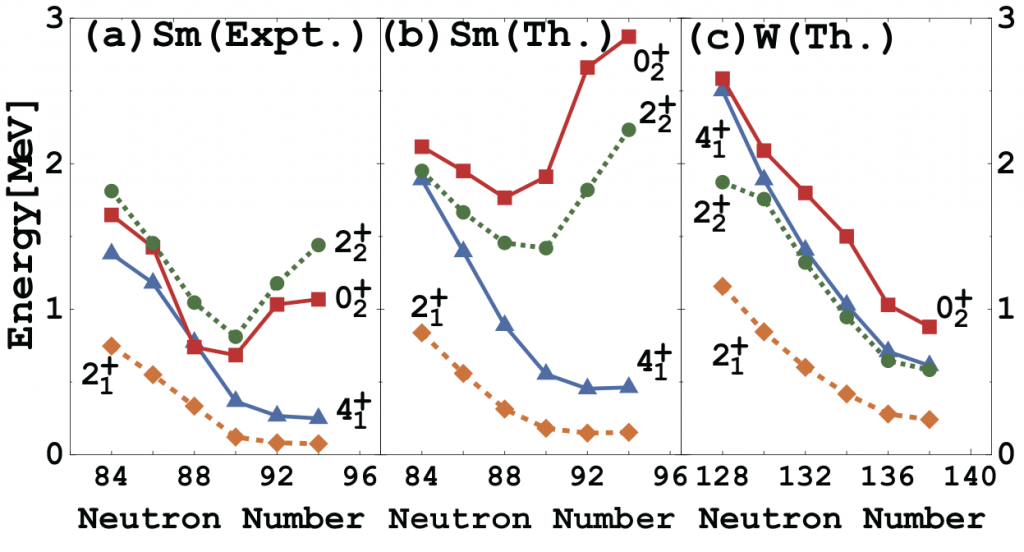
[1] K. Nomura, N. Shimizu, and T. Otsuka, Phys. Rev. Lett. 101 (2008) 142501
[2] K. Nomura, N. Shimizu, and T. Otsuka, Phys. Rev. C 81 (2010) 044307
[3] K. Nomura, T. Otsuka, N. Shimizu, and L. Guo, Phys. Rev. C 83 (2011) 041302(R)
[4] K. Nomura, N. Shimizu, D. Vretenar, T. Nikšić, and T. Otsuka, Phys. Rev. Lett. 108 (2012) 132501
Shape coexistence
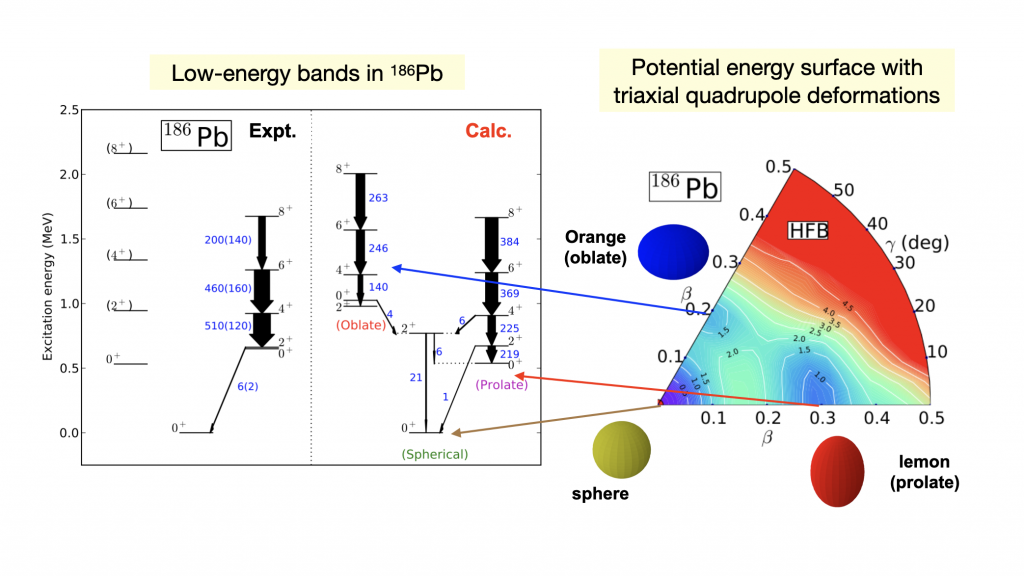
The phenomenon of shape coexistence is an intriguing feature of nuclei, in which competing intrinsic shapes appear near the ground state within a single nucleus. The manifestation of the shape coexistence is the emergence of low-lying excited 0+ states and subsequent bands. The extra low-spin states are considered to be the intruder states that arise from the multiparticle-multihole excitations across the major shell closure. The intruder configurations are also associated with certain intrinsic deformations indicated as different mean-field minima in the potential energy surface.
We have developed a method to study the phenomenon of shape coexistence from the point of view of the IBM in which the intruder configurations corresponding to the particle-hole excitations and the configuration mixing between the normal and intruder states are incorporated microscopically with the aid of the nuclear energy density functional (EDF) framework [1]. The EDF-based, configuration-mixing IBM allows for a plausible step toward a systematic and accurate theoretical description of the shape coexistence and related excited states, and has been employed to calculate the spherical-prolate-oblate shape coexistence in Pb-Hg region [1,2], and the shape phase transitions and coexistence in the neutron-rich nuclei in the mass A~100 region [3], which are experimentally of much interest.
Another relevant application of this method concerns the structure of the even-even cadmium (Cd) nuclei. The Cd isotopes have been a classic example for vibrational nuclei. Experiments suggest, however, additional low-lying states which could be attributed to cross-shell intruder excitations. Based on the microscopic EDF calculation as input to an IBM calculation, we have been able to identify possible intruder states in the energy spectra of even-even Cd isotopes [4].
References
[1] K. Nomura, R. Rodríguez-Guzmán, L.M. Robledo, and N. Shimizu, Phys. Rev. C 86 (2012) 034322
[2] K. Nomura, T. Otsuka, and P. Van Isacker, J. Phys. G 43 (2016) 024008
[3] K. Nomura, R. Rodríguez-Guzmán, and L.M. Robledo, Phys. Rev. C 94 (2016) 044314
[4] K. Nomura, and J. Jolie, Phys. Rev. C 98 (2018) 024303
Octupole deformations
Octupole, or pear-shaped, nuclear deformation is a topic that has been recurrently studied. Recent experiments using radioactive-ion beam have identified evidence for a stable octupole deformation. The related theoretical investigations have been extensively conducted using a variety of nuclear models. In addition, the presence of static octupole correlations in the nucleus enhances an atomic electric dipole moment (EDM). The observation of a non-zero EDM would imply the violation of the CP symmetry.
In addition to the positive-parity s-d bosons, we have included the negative-parity f (octupole) boson in the IBM space. Particularly, we have developed a way of determining the sdf-boson model Hamiltonian based on the quadrupole-octupole constrained mean-field calculations using a universal EDF. An illustrative application to the axially-symmetric light actinides and rare-earth nuclei [1,2] has show that the static octupole deformation appears in certain nuclei for which octupole shape is empirically suggested to be stabilized, and that the shape phase transitions occur that involve both the quadrupole and octupole degrees of freedom.
Furthermore, couplings between the octupole and additional degrees of freedom are incorporated in a microscopic manner in the IBM and shown to play an important role in the description of the related, intriguing nuclear structure phenomena, such as the low-spin band structure of odd-mass nuclei [3], and the shape coexistence [4].
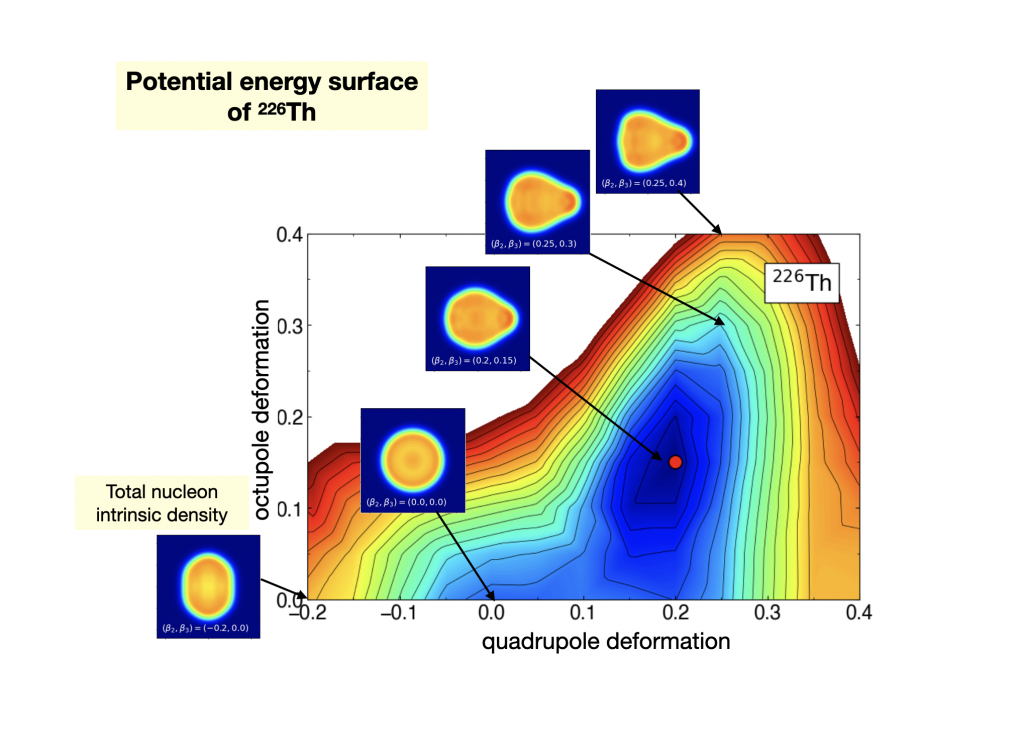
References
[1] K. Nomura, D. Vretenar, and B.-N. Lu, Phys. Rev. C 88 (2013) 021303(R)
[2] K. Nomura, D. Vretenar, T. Nikšić, and B.-N. Lu, Phys. Rev. C 89 (2014) 024312
[3] K. Nomura, T. Nikšić, and D. Vretenar, Phys. Rev. C 97 (2018) 024317
[4] K. Nomura, Phys. Rev. C 106 (2022) 024330
Fundamental nuclear processes
Nuclear β decay is a fundamental process in which protons in the nucleus convert into neutrons, or vice versa. The β decay is important for determining the low-lying structure of individual nuclei, and is also crucial to model astrophysical nucleosynthesis of heavy elements. In rare cases, two successive β decays may occur (double-β or ββ decay) between the neighboring even-even nuclei, emitting two electron or positrons and some light light particles. Especially the ββ decay that does not emit neutrinos (0νββ decay) is of fundamental importance, because this decay mode would imply violations of various symmetry properties required for the electroweak fundamental interaction.
In nuclear theory, calculations of the nuclear matrix elements for these fundamental nuclear decays require the precise modeling of the nuclear low-lying states for each nucleus involved in the process (even-even, odd-even, and odd-odd). By making use of the microscopic EDF and particle-boson core coupling, i.e., the Interacting Boson-Fermion Model (IBFM), we have developed a theoretical scheme that allows for a simultaneous description of the nuclear low-lying states and β decay properties. Within this scheme the Hamiltonian of the IBFM is obtained by using the inputs from the EDF calculation, and the resultant wave functions are used for computing the Gamow-Teller and Fermi transition matrix elements.
Using this method, the β decay properties for the odd- [1] and even-A [2] nuclei in the mass A~130 region, and the transitional nuclei Ge and As [3] have been studied. In [4], the two-neutrino ββ decays have been investigated for a large number of even-even nuclei, and this presents a benchmark for exploring the 0νββ decay, which is of much interest both experimentally and theoretically.
References
[1] K. Nomura, R. Rodríguez-Guzmán, and L.M. Robledo Phys. Rev. C 101 (2020) 024311
[2] K. Nomura, R. Rodríguez-Guzmán, and L.M. Robledo Phys. Rev. C 101 (2020) 044318
[3] K. Nomura, Phys. Rev. C 105 (2022) 044306
[4] K. Nomura, Phys. Rev. C 105 (2022) 044301
